Вычислительная часть сервера использует свободно распространяемый код программы EMAP4, основанной на векторном методе конечных элементов (FEM), используемом для решения неоднородного уравнения Гельмгольца для вектора электрического поля.
1. Входные файлы
Входные файлы программы - это текстовые файлы в формате SIF (Standard
Input File) [T. H. Hubing, C. Hong-Him Lim and J. Drewniak, "A
Geometry Description Language for 3D Electromagnetic Analysis Codes,"
Proceedings of the 10th Annual Review of Progress in Applied Computational
Electromagnetics, pp. 417-422, March 1994]. Входной файл может быть создан с
помощью простого текстового редактора или
непосредственно в текстовом поле рабочего окна пользователя. Программа автоматически
генерирует тетраэдральные сетки для метода конечных элементов, используя входные данные. Входной файл в стандартном формате
состоит из нескольких ключевых слов и их атрибутов.
Ниже дано детальное описание ключевых слов входного
файла:
1. #: Программа пропускает строки, начинающиеся с символа #. Он используется для добавления комментариев во входные файлы. Закомментированные строки появляются и в выходных файлах, делая удобным документирование результатов. Если первая строка входного файла является комментарием, то она используется сервером для идентификации задачи в процессе счета и просмотра списка результатов. Комментарии не должны содержать символов с кодами выше 127.
2. box: это ключевое слово обозначает полый проводящий параллелепипед. Программа присваивает нулевое значение тангенциальной составляющей электрического поля на поверхности этого параллелепипеда. В качестве атрибутов задаются координаты двух диагональных точек параллелепипеда: x1 y1 z1 x2 y2 z2. Координаты задаются целыми числами в единицах ячеек сетки (см. celldim).
3. celldim: по умолчанию размер сетки для FEM составляет 1 см вдоль каждой оси. Пользователь может изменить шаг сетки вдоль осей x, y, z, используя celldim. Например, следующая строка устанавливает шаг сетки равным 2 см вдоль оси x в интервале от x=0 до x=5: "celldim 0 5 2 cm". В качестве единиц могут быть указаны mm, cm, m или in (дюймы). Директивы celldim позволяют задавать неоднородные сетки, возможность использования которых является одним из преимуществ метода конечных элементов. Необходимо иметь в виду, что координаты всех объектов во входных файлах задаются в номерах ячеек сетки.
4. dielectric: обозначает диэлектрическую пластину. Шесть чисел определяют два диагональных угла пластины, следующие два атрибута обозначают диэлектрическую проницаемость и проводимость (мнимую часть комплексной проницаемости). Все величины – в единицах СИ.
5. PML: ключевое слово PML обозначает "идеально согласованный слой", который позволяет моделировать открытые электродинамические системы (см. Раздел 4). Шесть чисел определяют два узла на диагональных углах пластины. Дополнительные атрибуты относятся к свойствам идеально согласованного слоя. Два атрибута a и b по умолчанию равны 1.0. Следующий атрибут Dir может принимать одно из следующих значений: x, y, z - когда PML находится на соответствующей поверхности. Например, "x" будет гасить распространение волн в направлении x; xy, yz, xz, когда PML находится на ребре между двумя плоскостями; xyz - когда PML находится в углу.
6. conductor: проводник. Это может быть одномерный провод, двумерная пластина или трехмерный блок. Программа устанавливает значение электрического поля на всех граничных поверхностях проводника равным нулю. Поля внутри трехмерных проводников также устанавливаются равными нулю.
7. aperture: создает прямоугольную апертуру в проводящей стенке, координаты определяют 2 точки на поверхности стенки.
8. esource: задает электрическое поле вдоль ребер сетки. esource может быть одномерным, двумерным или трехмерным. Все ребра сетки внутри объема, поверхность или линия между двумя узлами инициализируются в соответствии с указанными атрибутами: частотой (в МГц), поляризацией (x, y или z) и комплексной амплитудой (действительная часть, мнимая часть).
9. isource: определяет источник тока. Координаты двух узлов определяют линию, на которой расположен источник, остальные атрибуты те же, что и в esource.
10. efield_output: определяет область, где будет выдаваться электрическое поле, и имя соответствующего выходного файла. Две точки определяют два узла в противоположных углах параллелепипеда (плоскости, линии), затем указывается название выходного файла. Например, efield_output 0 0 0 10 10 0 example.out заставит программу записать значения поля в узлах внутри прямоугольной области, определяемой двумя диагональными узлами (0, 0, 0) и (10, 10, 0), в файл example.out.
11. default_out: программа выдает значения поля вдоль всех ребер сетки в указанный файл. Например, default_out default.out печатает значения электрического поля вдоль всех ребер сетки в файл default_output (чтобы пользоваться информацией, записанной в этот файл, необходимо знать нумерацию ребер).
12. resistor: резистор. Координаты двух точек определяют узлы, между которыми подключен резистор, затем указывается сопротивление в омах.
13. freqstep: это ключевое слово позволяет за один пуск программы провести вычисления на нескольких частотах. Два атрибута задают количество шагов и шаг по частоте (в МГц). В качестве начальной частоты используется частота, указанная в esource или isource.
Сводная таблица ключевых слов и атрибутов входного файла:
| Ключевое слово | Координаты положения | Атрибуты |
| # | ||
| box | x1 y1 z1 x2 y2 z2 | |
| celldim | p1 p2 | направление величина единицы |
| PML | x1 y1 z1 x2 y2 z2 | направление a b |
| dielectric | x1 y1 z1 x2 y2 z2 | e s |
| aperture | x1 y1 z1 x2 y2 z2 | |
| conductor | x1 y1 z1 x2 y2 z2 | |
| esource | x1 y1 z1 x2 y2 z2 | частота поляризация (x, y или z) амплитуда |
| isource | x1 y1 z1 x2 y2 z2 | частота поляризация (x, y или z) амплитуда |
| efield_output | x1 y1 z1 x2 y2 z2 | имя файла |
| default_out | имя файла | |
| resistor | x1 y1 z1 x2 y2 z2 | сопротивление |
| freqstep | количество шагов шаг |
Пример входного файла.
Все координаты определяются во входном файле. Необходимо отметить, что координаты базируются на номерах ячеек, а не на физических размерах. Если необходимо изменить плотность сетки, то все координаты должны быть изменены. Простой пример - волновод, частично заполненный диэлектриком, показан на следующем рисунке, далее дан соответствующий входной файл.

# 8x4x5 waveguide half filled with a dielectric
# Default output written to file "default.out"
# Electric fields along axis written to "center.out"
# Electric fields along shifted axis written to "off_axis.out"
celldim 1 cm
box 0 0 0 8 4 5
dielectric 0 0 3 8 4 5 3.0
esource 4 0 2 4 4 2 1000 y 1.000 0
default_output default.out
efield_output 4 2 0 4 2 5 center.out
efield_output 2 2 0 2 2 5 off_axis.out
Первые четыре строки являются комментариями. Строка сelldim устанавливает
размер сетки равным 1 см. В строке "box" говорится, что внешняя оболочка –
проводник. Строка "dielectric" устанавливает свойства и расположение
диэлектрика. Строка "esource" определяет свойства и местонахождение источника
поля.
Строка "default_output" означает, что все значения электрического поля на выходе
программы будут записываться в файл "default.out". Строки "efield_output"
сообщают программе, что все выходные значения электрического поля внутри
заданного координатами объема должны записываться в указанный файл.
2. Выходные файлы
Выходные файлы имеют текстовый формат. В них помещаются строки - комментарии из входного файла, затем для каждого узла из заданной области выводится строка, состоящая из 9 чисел. Первые три числа - координаты узла (в метрах), затем идут три (x, y, z) комплексных амплитуды электрического поля в этом узле.
В этом разделе приведен ряд примеров, иллюстрирующих различные возможности
программы EMAP4. В первом наборе примеров используются идеальные волноводы и
проводится сравнение результатов работы программы с аналитическими решениями. Во
второй группе используется геометрия линии передачи. Результаты
EMAP4 сравниваются с результатами, полученными с помощью программы FASTCAP,
использующей метод моментов (MOM). Третий пример – резонатор, возбуждаемый
широкой пластиной. Этот пример используется для сравнения результатов
моделирования с экспериментальными данными. Эти примеры иллюстрируют большое
разнообразие возможных применений программы. Другая возможность программы –
использование идеально согласованного слоя для создания поглощающей границы.
Соответствующие примеры приведены в разделе 4.
Волноводы
Примеры этого раздела основаны на простых прямоугольных волноводах. Результаты
использования программы сравниваются с результатами аналитических расчетов.
Первый пример волновода показан на следующем рисунке.
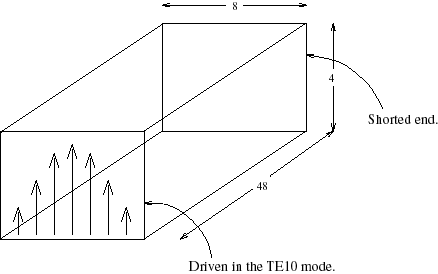
Поперечное сечение волновода 8 см на 4 см. Длина – 48 см. Частота возбуждения
1910 МГц. Волновод возбуждается с одного конца модой TE10 и закорочен на другом
конце. Волновод заполнен диэлектриком без потерь (e
= 2.0). Аналитические результаты получены с использованием теории волноводов в
предположении возбуждения моды TE10. Напряжение вдоль волновода дается формулой:
,
где g вычисляется по формуле:
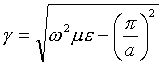
Это уравнение использовано для получения теоретической кривой,
показанной вместе с результатами моделирования на следующем
рисунке:
Видно, что имеется очень хорошее соответствие между результатами работы программы и теорией.
Во втором примере волновод из первого примера заполнен диэлектриком с потерями: диэлектрическая проницаемость e =3.0 и проводимость s=0.02. Аналитические результаты получены так же, как в первом примере. Здесь g представляется в виде a + jb. Результат показан на следующем рисунке:
Форма рассчитанной кривой очень хорошо совпадает с теоретической.
Входной файл для первого примера выглядит следующим образом:
# Waveguide driven in TE10 mode
celldim 1 cm
box 0 0 0 8 4 48
dielectric 0 0 0 8 4 48 2.0 0.0
esource 7 0 0 8 4 0 1910 y 0.1951 0
esource 6 0 0 7 4 0 1910 y 0.5556 0
esource 5 0 0 6 4 0 1910 y 0.8315 0
esource 4 0 0 5 4 0 1910 y 0.9808 0
esource 3 0 0 4 4 0 1910 y 0.9808 0
esource 2 0 0 3 4 0 1910 y 0.8315 0
esource 1 0 0 2 4 0 1910 y 0.5556 0
esource 0 0 0 1 4 0 1910 y 0.1951 0
esource 8 0 0 8 4 0 1910 y 0.0000 0
esource 7 0 0 7 4 0 1910 y 0.3830 0
esource 6 0 0 6 4 0 1910 y 0.7070 0
esource 5 0 0 5 4 0 1910 y 0.9240 0
esource 4 0 0 4 4 0 1910 y 1.0000 0
esource 3 0 0 3 4 0 1910 y 0.9240 0
esource 2 0 0 2 4 0 1910 y 0.7070 0
esource 1 0 0 1 4 0 1910 y 0.3830 0
esource 0 0 0 0 4 0 1910 y 0.0000 0
efield_output 0 2 0 8 2 48 example.out
Первая строка входного файла закомментирована. Строка "celldim" устанавливает
размер сетки равным 1 см во всех направлениях. Это составляет примерно 15 ячеек
на длину волны. В строке "box" определяется, что четыре боковые стороны
волновода и его задняя стенка – проводники. Передняя стенка – также проводящая,
но строки "esource" переопределяют тангенциальную составляющую электрического
поля на ней. Строка "dielectric" определяет положение и свойства диэлектрика (во
втором примере эта строка должна быть немного изменена, чтобы включить
проводимость). Строка "efield_output" сообщает программе, что требуемые значения
электрического поля должны записываться в файл example.out. Строки "esource"
требуются для генерации TE10 моды. Первый набор строк esource – двумерный и
инициализирует диагональные и недиагональные ребра на поверхности. Т.к. мы
инициализируем моду TE10 , величины электрического поля на диагональных ребрах
немного отличаются от значений на недиагональных ребрах (форма синусоиды).
Второй набор строк esource инициализирует недиагональные ребра. Величина
электрического поля в этом примере меняется от нуля на краях до 1 в середине .
Например, величина поля вдоль ребер x=2 устанавливается равной 0.707 и 0.9240
для x=3. Величина поля на диагональном ребре между ними составляет 0.8315. В
программе электрическое поле вдоль диагонального ребра инициализируется
величиной в
раз большей величины, заданной во входном файле. Диагональные ребра расположены
под углом 45 градусов по отношению к недиагональным, поэтому электрическое поле
вдоль них больше. Если сетка неоднородна, то угол наклона диагональных ребер
отличается от 45 градусов, и в этом случае диагональные ребра должны быть
инициализированы по-другому.
Линии передач
В этом разделе рассматриваются простые прямоугольные линии передачи. Линия передачи имеет центральный сплошной проводник и внешний проводник, параллельный поверхности внутреннего проводника. Такая линия показана на следующем рисунке:
Линия передачи возбуждается источником напряжения (электрическим полем) на одном конце и заканчивается резисторами на противоположном конце. Для вычисления емкости на единицу длины используется численный метод FASTCAP. Характеристический импеданс линии определяется выражением:
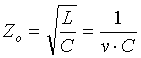
где v = 3ґ 108 м/с. Эта величина сравнивается с характеристическим импедансом, полученным с использованием EMAP4. Характеристический импеданс определяется путем изменения величины концевых резисторов таким образом, чтобы амплитуда электрического поля вдоль линии оказалась постоянной. В следующей таблице показаны различные анализируемые конфигурации.
| Сторона внутреннего проводника | Сторона внешнего проводника | FASTCAP характ. имп (Ом) | EMAP4 характ. имп. (Ом) |
| 1 см | 3 см | 48 | 50 |
| 2 см | 4 см | 31 | 33 |
| 3 см | 5 см | 23 | 25 |
На следующем рисунке показан пример зависимости электрического поля от положения вдоль линии. В этом примере ширина внутреннего проводника – 1 см, а внешнего – 3 см.
Теоретическая кривая получается с использованием характеристического
импеданса, полученного в FASTCAP. Она определяется выражением:
Корреляция в этом примере очень хорошая. Причиной расхождения могут быть
несколько факторов. Концевые резисторы могут неточно отражать характеристический
импеданс из-за положения и числа резисторов. Моделирование резисторов не может
быть очень точным. Форма кривой также чувствительна к малым изменениям величины
резисторов, величин используемой магнитной и диэлектрической проницаемости.
Входной файл для этого примера выглядит следующим образом:
celldim 1 cm
box 0 0 0 3 3 24
aperture 0 0 0 3 3 0
aperture 0 0 24 3 3 24
conductor 1 1 0 2 2 24
esource 1 0 0 1 1 0 1000 y -1.0 0.0
esource 2 0 0 2 1 0 1000 y -1.0 0.0
esource 2 1 0 3 1 0 1000 x 1.0 0.0
esource 2 2 0 3 2 0 1000 x 1.0 0.0
esource 1 2 0 1 3 0 1000 y 1.0 0.0
esource 2 2 0 2 3 0 1000 y 1.0 0.0
esource 0 1 0 1 1 0 1000 x -1.0 0.0
esource 0 2 0 1 2 0 1000 x -1.0 0.0
resistor 1 0 24 1 1 24 600
resistor 2 0 24 2 1 24 600
resistor 2 1 24 3 1 24 600
resistor 2 2 24 3 2 24 600
resistor 1 2 24 1 3 24 600
resistor 2 2 24 2 3 24 600
resistor 0 1 24 1 1 24 600
resistor 0 2 24 1 2 24 600
efield_output 2 1 0 2 1 24 tline.out
Строка "celldim" определяет размер ячейки, равным 1 см во всех направлениях.
Строка "box" определяет шесть поверхностей внешнего проводника. Строка "aperture"
переопределяет переднюю и заднюю поверхности "box".
Строка "conductor" инициализирует внутренний проводник. Строка "esource"
инициализирует источник поля, устанавливая поле между внутренним и внешним
проводником постоянным. Строка "resistor" устанавливает величины сопротивления
концевых резисторов. Требуемая величина концевой нагрузки составляет 75 Ом.
Поскольку число резисторов равно 8, то каждый из них должен иметь величину 600
Ом. Поле вдоль линии внутри линии передачи записывается в выходной файл
tline.out.
Объемный резонатор
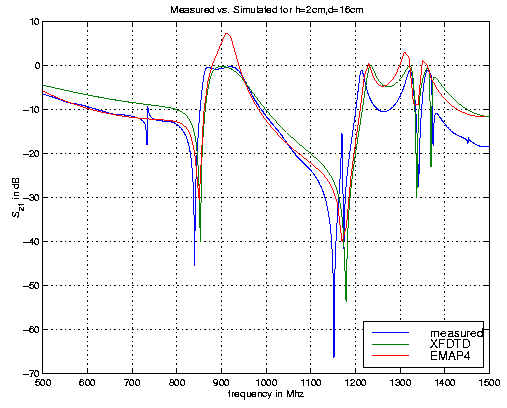
В этом разделе описываются попытки моделировать простой резонатор. Резонатор показан на следующем рисунке:
Это прямоугольный резонатор, который подключен к анализатору двумя кабелями. Между двумя вводами находится пластина шириной 16 см, она расположена на высоте 2 см от плоскости, через которую вводятся кабели. Пластина моделируется двумерным проводником. Возбуждающий ввод моделируется как "isource". Нагрузка на другом вводе моделируется двумя 25-омными последовательно соединенными резисторами. Коэффициент передачи S21 вычисляется путем деления напряжения на 50–омной нагрузке на входное напряжение (напряжение на "isource"). На следующем рисунке результаты, полученные с помощью программы EMAP4, сравниваются с экспериментально измеренными значениями коэффициента передачи. Приведены также результаты моделирования с использованием программы XFDTD.
На следующем рисунке сравниваются результаты EMAP4, XFDTD и измерений при расстоянии от плоскости вводов до пластины, равном 4 см.
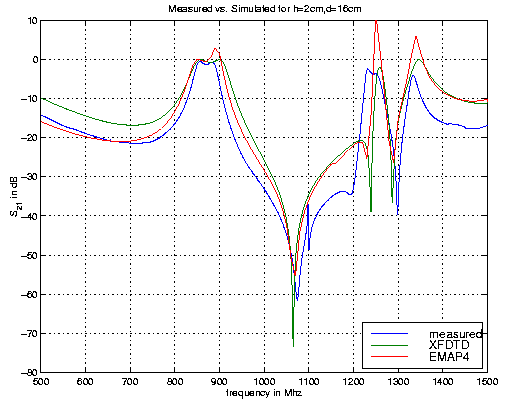
Хотя согласие довольно хорошее, у модели есть несколько недостатков. Первое –
не учитывается толщина подводящих кабелей, подсоединенных к пластине. Во-вторых,
источник и нагрузка моделируются не полностью.
4. Идеально согласованный слой (PML)
Примеры
Этот раздел иллюстрирует использование идеально согласованного слоя (PML - perfectly matched layer) на одномерном примере, показанном на следующем рисунке:
Прямоугольный волновод заканчивается идеально согласованным слоем на одном конце (за слоем расположена проводящая стенка). Волновод возбуждается модой TE10 на другом конце. Волновод заполнен диэлектриком без потерь. Входной файл для данного примера выглядит следующим образом:
# Waveguide driven in TE10 mode
# The waveguide is terminated in a PML
# The PML is backed by an electric wall
celldim 1 cm
box 0 0 0 8 4 48
PML 0 0 36 8 4 48 z 1.0 1.0
esource 7 0 0 8 4 0 1910 y 0.1951 0
esource 6 0 0 7 4 0 1910 y 0.5556 0
esource 5 0 0 6 4 0 1910 y 0.8315 0
esource 4 0 0 5 4 0 1910 y 0.9808 0
esource 3 0 0 4 4 0 1910 y 0.9808 0
esource 2 0 0 3 4 0 1910 y 0.8315 0
esource 1 0 0 2 4 0 1910 y 0.5556 0
esource 0 0 0 1 4 0 1910 y 0.1951 0
esource 8 0 0 8 4 0 1910 y 0.0000 0
esource 7 0 0 7 4 0 1910 y 0.3830 0
esource 6 0 0 6 4 0 1910 y 0.7070 0
esource 5 0 0 5 4 0 1910 y 0.9240 0
esource 4 0 0 4 4 0 1910 y 1.0000 0
esource 3 0 0 3 4 0 1910 y 0.9240 0
esource 2 0 0 2 4 0 1910 y 0.7070 0
esource 1 0 0 1 4 0 1910 y 0.3830 0
esource 0 0 0 0 4 0 1910 y 0.0000 0
efield_output 0 2 0 8 2 48 example.out
В строке "celldim" размер ячейки сетки устанавливается равным 1 см во всех
направлениях. Это составляет примерно 15 ячеек на длину волны. Строка "box"
устанавливает, что четыре боковые стенки и задняя стенка волновода являются
проводниками. Передняя стенка также объявляется проводником, но переопределяется
в строке "esource". Строка "PML" содержит информацию о
положении и свойствах идеально согласованного слоя. Строки " esource" генерируют
TE10 моду (см. Раздел 3). Строка "efield_output " выводит значения
электрического поля вдоль оси волновода в файл. Как видно из входного файла,
длина волновода 46 см, а длина идеально согласованного слоя 12 см (эта величина
варьируется). Длина волновода составляет примерно 2l,
длина идеально согласованного слоя примерно 0.75l. В
этом примере длина идеально согласованного слоя может меняться, а оставшаяся
длина остается постоянной. Изучаются различные аспекты идеально согласованного
слоя.
Влияние числа идеально согласованных слоев на коэффициент отражения.
Результаты показаны на следующем рисунке. Видно, что отражение уменьшается
по мере увеличения числа слоев.
Влияние величин a и b
на отражение.
Результаты показаны на следующем рисунке. Как видно, коэффициент отражения
сначала уменьшается с увеличением b, достигает
минимума, а затем снова увеличивается. Характеристика улучшается, когда
a устанавливается равным b.
Число требуемых итераций.
Программа использует комплексный би-сопряженный метод решения системы
линейных уравнений. Возникает вопрос: как величины a
и b влияют на скорость сходимости (число
обусловленности) алгоритма? Следующий рисунок проясняет это. Видно, что большие
величины a и b
уменьшают скорость сходимости.
|
|